Answer:
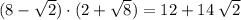 .
.
Explanation:
Step One: Simplify the square roots.
 .
.
The square root of 8
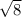 can be simplified as the product of an integer and the square root of 2:
can be simplified as the product of an integer and the square root of 2:
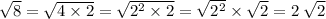 .
.
As a result,
 .
.
Step Two: Expand the product of the two binomials.
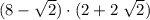 is the product of two binomials:
is the product of two binomials:
- Binomial One:
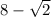 .
. - Binomial Two:
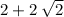
Start by applying the distributive law to the first binomial. Multiply each term in the first binomial (without brackets) with the second binomial (with brackets)
![({\bf 8} - {\bf √(2)}) \cdot {(2 + 2\; √(2))}\\= [{\bf 8} \cdot {(2 + 2\; √(2))}] - [{\bf √(2)} \cdot {(2 + 2\; √(2))}]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/lq1dgtyqdofpadktx3h1xa4ub9e66vwig2.png)
Now, apply the distributive law once again to terms in the second binomial.
![[8 \cdot ({\bf 2} + {\bf 2\; √(2)})] - [√(2) \cdot ({\bf 2} + {\bf 2\; √(2)})]\\= [8 * {\bf 2} + 8 * {\bf 2\;√(2)}] - [√(2) * {\bf 2} + √(2) * {\bf 2\; √(2)}]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/lq6ptemyvnbdapsd2gzz2qbc4g7af6dd6m.png) .
.
Step Three: Simplify the expression.
The square of a square root is the same as the number under the square root. For example,
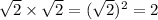 .
.
![[8 * 2 + 8 * 2\;√(2)] - [√(2) * 2 + 2 √(2) * √(2)]\\ =[16 + 16 \;√(2)] - [2 \;√(2) + 4]\\= 16 + 16\;√(2) - 2\; √(2) - 4](https://img.qammunity.org/2020/formulas/mathematics/middle-school/l22kt1gl5xipgg3wp8z8l6327vn1qrqmqr.png) .
.
Combine the terms with the square root of two and those without the square root of two:
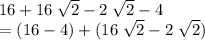 .
.
Factor the square root of two out of the second term:
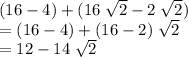 .
.
Combining the steps:
![(8 - √(2)) \cdot (2 + 2\; √(2))\\= [8 \cdot (2 + 2\; √(2))] - [√(2) \cdot (2 + 2\; √(2))]\\= [8 * 2 + 8 * 2\;√(2)] - [√(2) * 2 + √(2) * 2 \;√(2)]\\= [16 + 16 \;√(2)] - [2 \;√(2) + 2 * (√(2))^(2)]\\= [16 + 16 \;√(2)] - [2 \;√(2) + 2 * 2]\\= [16 + 16 \;√(2)] - [2 \;√(2) + 4]\\= 16 + 16\;√(2) - 2\; √(2) - 4\\= (16 - 4) + (16 \; √(2) - 2\; √(2))\\](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1oc5dox39308ju1epzy0okt9ihr07u4m1i.png)
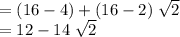 .
.