Answer:
a. d =

b. d =
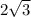
c. d =
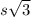
Explanation:
to find the length of the longest diagonal of the cube at first you will find the length of the diagonal if its base
If the length of the side of a cube is x
∴the length of the diagonal of the base =

Now to find the length of the longest diagonal we will use Pythagoras with the side of the cube and the diagonal of the base

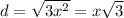
means the length of the side multiply by root 3
a. The length of the side is 1 so
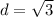
b. The length of the side is 2 so
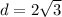
c. The length of the side is s so
