Answer:
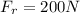
Step-by-step explanation:
Given
Let the two forces be
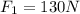

and
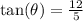
Required
Determine the resultant force
Resultant force (Fr) is calculated using:

This means that we need to first calculate
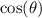
Given that:
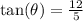
In trigonometry:
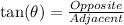
By comparing the above formula to
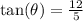
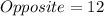
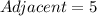
The hypotenuse is calculated as thus:
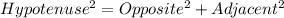
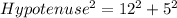
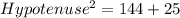
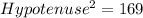
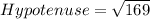
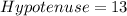
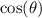 is then calculated using:
is then calculated using:
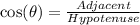
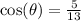
Substitute values for
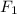 ,
,
 and
and
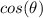 in
in


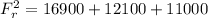
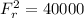
Take square roots of both sides
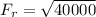
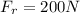
Hence, the resultant force is 200N