Question

Given that QT is and altitude of triangle QRS and that m

Answer 1

Hello from MrBillDoesMath!

Answer:

15

Discussion:

Given: measure angle STQ = 7x + 55. But, as shown, STQ is a right angle so

7x + 55 = 90 => subtract 55 from each side

7x = 90 -55 = 35 => divide each side by 7

x = 35/7 = 5

Since RS = (x+1) + (2x-1) where x = 5.

RS = (5 + 1) + (2*5 -1)

= 6 + 9

= 15

I don't know what choice the answer is as your diagram only shows Choice A

Thank you,

MrB

Answer 2

`RS=15`

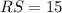
Explanation:

We have been given a triangle. We are asked to find the measure of segment RS.

Since QT is altitude of our given triangle, so angle QTR and angle QTS are right triangles.

Let us solve for x by equating measure of angle STQ with 90 degrees.

`m\angle STQ=90`

`7x+55=90`

`7x+55-55=90-55`

`7x=35`

`(7x)/(7)=(35)/(7)`

`x=5`

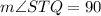
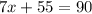
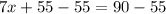
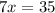
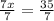
We can see that segment RS is RT plus TS.

`RS=RT+TS`

`RS=x+1+2x-1`

`RS=x+2x`

`RS=3x`

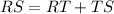
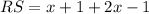
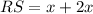
Upon substituting
`x=5`, we will get:

`RS=3*5`

`RS=15`

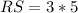
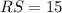
Therefore, the length of segment RS is 15 units.