Question

The areas of two similar triangles are 72dm2 and 50dm2. The sum of their perimeters is 226dm. What is the perimeter of each of these triangles?

Answer 1

Hence, the perimeter of the triangles are:

P=123.2727 dm

P'=102.7272 dm

Explanation:

In two similar triangles:

The ratio of the areas of two triangle is equal to the square of their perimeters.

Let A and A' represents the area of two triangles and P and P' represents their perimeter.

Then they are related as:

`(A)/(A')=(P^2)/(P'^2)`

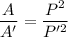
We are given:

A=72 dm^2 , A'=50 dm^2

and P+P'=226 dm.-----------(1)

i.e.
`(72)/(50)=(P^2)/(P'^2)\\\\(36)/(25)=(P^2)/(P'^2)`

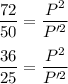
on taking square root on both the side we get:

`(P)/(P')=(6)/(5)\\\\P=(6)/(5)P'`

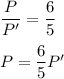
Now putting the value of P in equation (1) we obtain:

`(6)/(5)P'+P'=226\\\\(6P'+5* P')/(5)=226\\\\(6P'+5P')/(5)=226\\\\11P'=226* 5\\\\11P'=1130\\\\P'=(1130)/(11)=102.7272`

Hence,

P=226-102.7272=123.2727

Hence, the perimeter of the triangles are:

P=123.2727 dm

P'=102.7272 dm