Question

Which rules of exponents will be used to evaluate the expression. Check all that apply

Answer 1

Three rules are used

1) Product of powers

2) Power of a power

3) Negative exponents

Step-by-step explanation:

The given expression is [(7)⁵(7)³]⁻⁴

To find the value of [(7)⁵(7)³]⁻⁴

[(7)⁵(7)³]⁻⁴ = [(7)⁵⁺³]⁻⁴ = [(7)⁸]⁻⁴(using product of powers rule)

[(7)⁵⁺³]⁻⁴ = [(7)⁸ˣ⁻⁴] = 7⁻³² [using powers of power rule)

7⁻³² = 1/7³² (using negative exponent rule)

Using three rules we can solve [(7)⁵(7)³]⁻⁴

Therefore the correct answers are

1) Product of powers

2) Power of a power

3) Negative exponents

Answer 2

Hello!

The answer are:

- Product of powers.

- Power of a power.

- Negative exponents.

Why?

Let's solve it!

It's a math rule that we must solve first what's into a brake or parenthesis, so,

First: Product of powers
`[(7)^(5)*(7)^(3)]`

According to the exponent's law, we have a product of powers case, so, we need to sum the exponents and keep the base

Exponents: 5 and 3

Base: 7

Applying it we have:

`(7)^(5+3)`

`(7)^(8)`

Then,

We have a power of a power case, which involves multiplying the exponents:

`[(7)^(5)*(7)^(3)]^(-4)`

Exponents: 3 and -4

Then,

`(7)^(8*-4)`

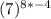
Finally, we can apply the negative exponents, the negative exponent's rules state that negative exponents are the reciprocal of the positive exponents,

So, we will have that:

`(7)^(-32)=(1)/(7^(32) )`

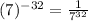
Have a nice day!