Question

Which of the following functions have graphs that contain no asymptotes? select all that apply

Answer 1

Explanation:

The graph of the power function has no asymptotes. Check this one.

The graph of the reciprocal function DOES have asymptotes, both vertical and horizontal. Do not check this function.

The graph of an exponential function has one asymptote, which is the line y = 0 (that is, the x-axis). Do not check this function.

The graph of a log function has one asymptote, which is the line x = 0 (that is, the y-axis). Do not check this function.

The root function does not have asymptotes. Check this function.

Answer 2

The power function and the root function

Explanation:

Let's consider each function in turn.

Power function

y = xⁿ

For every value of x, there is a corresponding value of y.

There are no asymptotes.

Reciprocal

y = 1/x

The y-axis is an asymptote, because x cannot equal 0. y ⟶ ∞ as x ⟶ 0₊ and y ⟶ -∞ as x ⟶ 0₋

Similarly, the x-axis is an asymptote, because there is no finite value of x for which y = 0.

Exponential

`y = b^(x)`

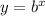
The x-axis is an asymptote, because y can never be negativeand y ⟶ 0

as x ⟶ -∞.

Logarithmic

`y = \text{log}_(b)(x)`

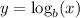
The y-axis is an asymptote, because x cannot be negative and logx ⟶ -∞ as x ⟶ 0.

Root

y = \sqrt[5]{x}

There can be no negative value of x, but there is a value of y for every positive value of x.

Thus, there is no asymptote.

The power function and the root function have no asymptotes.