Question

If the magnitude of the electric field in air exceeds roughly 3 ✕ 106 n/c, the air breaks down and a spark forms. for a two-disk capacitor of radius 69 cm with a gap of 1 mm, what is the maximum charge (plus and minus) that can be placed on the disks without a spark forming (which would permit charge to flow from one disk to the other)?

Answer 1

Answer: 39.8 μC

Explanation:

The magnitude of the electric field generated by a capacitor is given by:

`E = (V)/(d)`

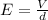
d is the distance between the plates.

For a capacitor, charge Q = CV where C is the capacitance and V is the voltage.

`C =(\epsilon_o A )/(d)`

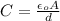
where A is the area of the plate and ε₀ is the absolute permittivity.

substituting, we get

`E = (Q)/(\epsilon_o A)`

It is given that the magnitude of the electric field that can exist in the capacitor before air breaks down is, E = 3 × 10⁶ N/C.

radius of the plates of the capacitor, r = 69 cm = 0.69 m

Area of the plates, A = πr² = 1.5 m²

Thus, the maximum charge that can be placed on disks without a spark is:

Q = E×ε₀×A

⇒ Q = 3 × 10⁶ N/C × 8.85 × 10⁻¹² F/m × 1.5 m² = 39.8 × 10⁻⁶ C = 39.8 μC.