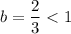Question

Which function represents exponential decay?

Answer 1

Option: D is the correct answer.

D)
`f(x)=4\cdot ((2)/(3))^x`

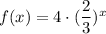
Explanation:

We know that a exponential function is in general represented by:

`f(x)=ab^x`

where a>0 and b is called the base of the function and x is the exponent.

and if b>1 then the function is a exponential growth function

and 0<b<1 then the function is a exponential decay function.

A)

`f(x)=(1)/(2)\cdot ((3)/(2))^x`

This is a exponential growth function.

Since,

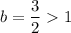
`b=(3)/(2)>1`

B)

`f(x)=(1)/(2)\cdot ((-3)/(2))^x`

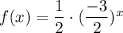
This is not a exponential function because b is not strictly greater than zero.

C)

`f(x)=4\cdot ((-2)/(3))^x`

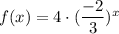
This is also not a exponential function because b is not strictly greater than zero.

D)

`f(x)=4\cdot ((2)/(3))^x`

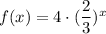
This is a exponential decay function.

Because it fulfills the condition of the exponential decay function.

Since,

`b=(2)/(3)<1`

Answer 2

D

Explanation:

Exponential decay occurs when the base is less than 1 but greater than 0.

3/2 = 1.5 and is greater than 1.

-3/2 is not greater than 0 and is not exponential

-2/3 is not greater than 0 and is not exponential

2/3 is less than 1 and greater than 0. This is decay.