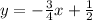Question

PLEASE HELP

Show all work to write the equations of the lines, representing the following conditions, in the form y = mx + b, where m is the slope and b is the y-intercept:

Part A: Passes through (−2, 2) and parallel to 4x − 3y − 7 = 0 (2 points)

Part B: Passes through (−2, 2) and perpendicular to 4x − 3y − 7 = 0 (2 points)

Answer 1

Part A
The given line passes through (-2,2) and it is parallel to the line


`4x - 3y - 7 = 0`


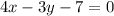
We need to determine the slope of this line by writing it in slope -intercept form.



`3y = 4x - 7`



`y = (4)/(3) x - (7)/(3)`
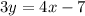
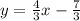
The slope of this line is

`(4)/(3)`


The line parallel to this line also has slope


`m = (4)/(3)`


The equation is


`y = (4)/(3) x + c`


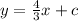
We substitute (-2,2)


`2 = (4)/(3)( - 2) + c`



`c = 2 + (8)/(3) = (14)/(3)`


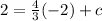
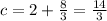
The required equation is



`y = (4)/(3) x + (14)/(3)`


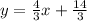
PART B


The given line is



`4x - 3y - 7 = 0`




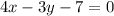
The slope of this line is

`(4)/(3)`


The slope of the line perpendicular to it is


`m = - (3)/(4)`

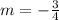
The equation of the line is


`y = - ( 3)/(4) x + c`




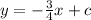
We substitute the point, (-2,2)




`2= - ( 3)/(4) ( - 2) + c`



`2= ( 3)/(2) + c`




`c = 2 - (3)/(2) = (1)/(2)`


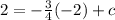
The equation of the perpendicular line is



`y= - ( 3)/(4) x + (1)/(2)`