Question

(PLEASE HELP )Use the discriminant to find the number of real solutions of the equation 3x^2-5x+4=0. show your work.

Answer 1

0

Explanation:

`\text{Use the discriminant:}\\\\ax^2+bx+c=0\\\\\Delta=b^2-4ac\\\\\text{If}\ \Delta>0\ \text{then the equation has two real solutions:}\ x=(-b\pm\sqrt\Delta)/(2a)\\\text{If}\ \Delta=0\ \text{then the equation has one real solution:}\ x=(-b)/(2a)\\\text{If}\ \Delta<0\ \text{then the equation has no solution.}`

`\text{We have the equation:}\\\\3x^2-5x+4=0\\\\a=3,\ b=-5,\ c=4\\\\\Delta=(-5)^2-4(3)(4)=25-48=-23<0\\\\\text{no solution}`

Answer 2

0 real solutions

Explanation:

The discriminant (D) is given by the formula:

`D=b^2-4ac`

Where a,b, and c are gotten from the standard form of a quadratic equation, which is
`ax^2+bx+c=0`

The equation given is
`3x^2-5x+4=0`

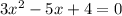
From this we can say that a = 3, b = -5, & c = 4. Plugging these into the discriminant formula we get:

`D=b^2-4ac\\D=(-5)^2-4(3)(4)\\D=-23`

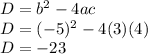
There are 3 things that we can find from the value of discriminant:

1. If D=0, there are 2 equal, real roots

2. if D>0, there are 2 distinct real roots

3. if D<0, there are no real roots, rather 2 imaginary roots

Since the value of the discriminant is negative (D<0), we can say that there are no real solutions for the equation given.