Question

A circle is centered at the point (5,-4) and passes through the point (-3,2)

Answer 1

The equation of the circle is

`(x-5)^(2) +(y+4)^(2)=100`

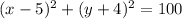
Explanation:

we know that

The equation of the circle in center radius form is equal to

`(x-h)^(2) +(y-k)^(2)=r^(2)`

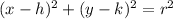
In this problem we have

`(h,k)=(5,-4)`

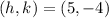
so

`(x-5)^(2) +(y+4)^(2)=r^(2)`

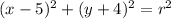
To find the radius substitute the value of x and the value of y of the point
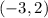`(-3,2)` in the equation

`(-3-5)^(2) +(2+4)^(2)=r^(2)`

`(-8)^(2) +(6)^(2)=r^(2)`

`100=r^(2)`

`r=10\ units`

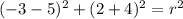
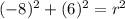
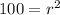
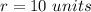
substitute

`(x-5)^(2) +(y+4)^(2)=10^(2)`

`(x-5)^(2) +(y+4)^(2)=100`

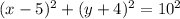
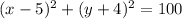
see the attached figure to better understand the problem