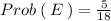Answer:
Probability of sum of pips on two faces is at least 9 =

Explanation:
Experiment: Throwing two fair dice.
Total no of Outcome =
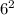 = 36
= 36
Sample space (list of outcome) is attached.
Let E be the event that sum of pips on two faces is at least 9.
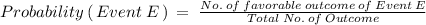
Favorable outcome are where sum is 9 , 10 , 11 and 12.
From Sample space, No. of Favorable outcome = 10
∴