Answer:
![4\sqrt[6]{x^5}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/w1vshqnu0ew0bpvulllo5jt2awtz48wewr.png)
Explanation:
A rational exponent is a fraction. The denominator of the fraction is the index of the root. The numerator of the fraction is an exponent.
Rule:
![a^{(m)/(n)} = \sqrt[n]{a^m}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mk71291k1pp22jvm1y2daukmo63331l7ej.png)
Notice that n, the denominator of the exponent is now the index of the root. The numerator of the fraction is an exponent.
Let's look at your case.
Only the variable x is raised to the exponent 5/6. The coefficient 4 is not being raised to the exponent 5/6.
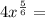

![= 4\sqrt[6]{x^5}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/aucev9fzvpclgi8e5lt66a8icvf8san8d7.png)