Question

Find the solution of ___ and determine if it is an extraneous solution

Answer 1

x = 14 is an extraneous solution

Explanation:

`4√(x + 2) = -16`

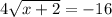
Divide both sides by 4.

`√(x + 2) = -4`

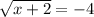
Square both sides.

`(√(x + 2))^2 = (-4)^2`

`x + 2 = 16`

`x = 14`

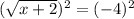
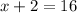
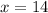
Since we squared both sides, we much check for extraneous solutions because the process of squaring both sides can introduce extraneous solutions.

Check x = 14:

`4√(x + 2) = -16`

`4√(14 + 2) = -16`

`4√(16) = -16`

`4(4) = -16`

`16 = -16`

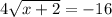
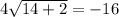
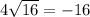
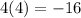
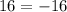
16 = -16 is a false statement, so the solution we found, x = 14, is an extraneous solution.