ANSWER
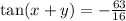
EXPLANATION
We were given that,
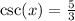
This implies that,
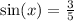
We use the Pythagorean identity
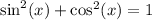
to get,

We were also given that,
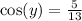
This means that,
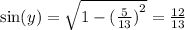
This is because,
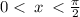

This angles are in the first quadrant so we pick the positive values.
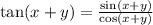
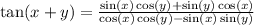
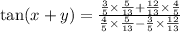
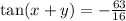
The correct answer is D