Answer: m∠
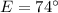
Explanation:
1. By definition, the adjacent angles of a parallelogram are supplementary, they add up 180 degrees. Therefore, in the given parallelogram:
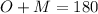
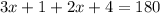
2. Then, you must solve for x, as following:
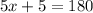

3. Substitute the value of x obtained into
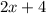 to calculate the angle M:
to calculate the angle M:
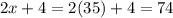
Then:
m∠
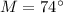
4. By definition the opposite angles of a parallelogram are equal, therefore:
