Question

The United States population of gray wolves was 1170 in 1991. If the population is decreasing by 5% each year, how long before there are only 300 left?

Answer 1

27 years.

Explanation:

We have been given that the United States population of gray wolves was 1170 in 1991. The population is decreasing by 5% each year.

We can see that population of grey wolves is decreasing exponentially, so we will use an exponential function to model the population after x years.

Since we know that exponential function is in form:
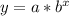`y=a*b^x`, where,

a = Initial value,

b = For decay b is in form (1-r), where r represents decay rate in decimal form.

Let us convert our given decay rate in decimal form.

`5\%=(5)/(100)=0.05`

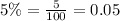
Upon substituting our given values we will get our function as:

`y=1170(1-0.05)^x`

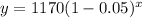
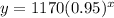`y=1170(0.95)^x`, where x represents number of years.

To find the time it will take the population to reach 300 we will substitute y=300 in our function.

`300=1170(0.95)^x`

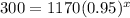
Let us divide both sides of our equation by 1170.

`(300)/(1170)=(1170(0.95)^x)/(1170)`

`0.2564102564102564=(0.95)^x`

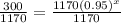
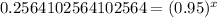
Let us take natural log of both sides of our equation.

`ln(0.2564102564102564)=ln((0.95)^x)`

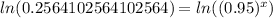
Using natural log property
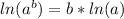`ln(a^b)=b*ln(a)` we will get,

`ln(0.2564102564102564)=x*ln(0.95)`

`(ln(0.2564102564102564))/(ln(0.95))=(x*ln(0.95))/(ln(0.95))`

`(-1.3609765531356007834)/(-0.0512932943875505)=x`

`x=26.53322\approx 27`

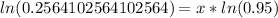
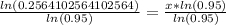
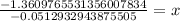
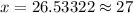
Therefore, it will take approximately 27 years to the population of grey wolves to reach 300.