Answer:
The rate of his boat is:
6 mph
Explanation:
It is given that:
Ben's boat will take 1 1/2 hours longer to go 12 miles up a river than to return.
Let u denote the speed of the boat in still water.
and v denote the speed of the current.
Then the speed of boat upstream= u-v km/h
and speed of boat downstream=u+v km/h
Let t denote the time taken by the boat downstream.
Then the time taken by boat upstream is: t+(3/2) hours
Distance traveled by boat each way is: 12 miles.
Hence, we have:
Speed of boat upstream is:
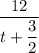
i.e.
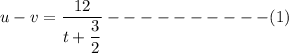
and
speed of boat downstream i.e.
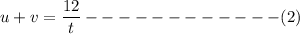
On subtracting equation (1) from equation (2) we have:

Also, we are given :
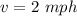
i.e.
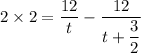
i.e.
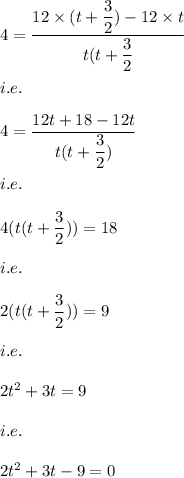
i.e.
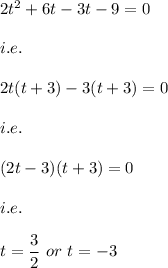
But t can't be negative.
Hence, we have:

Hence, from equation (2) we have:
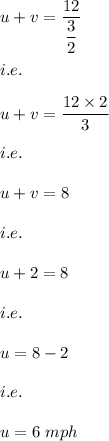
Hence, the answer is: 6 mph