Answer:
After 14 years, the area will be 2342.4 km squared.
Explanation:
Since the area is decreasing, we can use the decaying exponential function
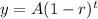
where
- A represents the initial area.
- r represents the rate at which the area changes
Given
Initial Area A = 4000 km squared
Rate r = 3.75% = 3.75/100 = 0.0375
Time period t = 14
To Determine
The Area after 14 years = y = ?
Plug in the values in the formula
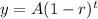
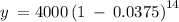
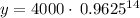
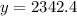 km squared
km squared
Therefore, after 14 years, the area will be 2342.4 km squared.