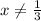Determine whether each function has an inverse function. If it does, find the inverse function and state any restrictions on its domain. 1. f(x) = |x-6| 2. f(x) = \sqrt[]{6 -x^(…

Question

Determine whether each function has an inverse function. If it does, find the inverse function and state any restrictions on its domain.

1.
`f(x) = |x-6|`

2.
`f(x) = \sqrt[]{6 -x^(2) }`

3.
`h(x) = (x+4)/(3x-5)`

Answer 1

QUESTION 1

The given function is;


`f(x) = |x - 6|`

This is an absolute value function.

For this function to have an inverse it must be a one-to-one function.

This absolute value function is not one-to-one
because


`f( 5)=1`
and


`f(7) = 1`

Since this function has more than one x-value mapping onto one y-value, it is not one-to-one and cannot have an inverse.

You can see from the graph that this function cannot pass the horizontal line test.

QUESTION 2

The given function is


`f(x) = \sqrt{6 - {x}^(2) }`

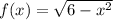
Let


`y= \sqrt{6 - {x}^(2) }`

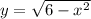
This implies that,


`{y}^(2) + {x}^(2) = 6`

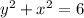
We see clearly that, this function is a circle that is centered at the origin.

This means that,


`f(x) = \sqrt{6 - {x}^(2) }`

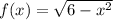
is a semicircle.

This function will not pass the horizontal line test and hence does not have an inverse.

QUESTION 3

The given function is


`h(x) = (x+4)/(3x-5)`

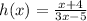
If we put


`h(a) = h(b)`

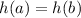
We obtain,


`(a+4)/(3a-5) = (b+4)/(3b-5)`


`(a + 4)(3b - 5) = (b + 4)(3a - 5)`


`3ab - 5a + 12b - 20 = 3ab - 5b + 12a - 20`


`- 17a = - 17b`


`a = b`

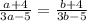
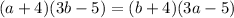
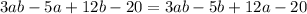
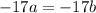
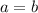
This shows that h(x) has an inverse because it is one-to-one.

Let


`y=(x+4)/(3x-5)`

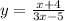
We interchange x and y to get,


`x=(y+4)/(3y-5)`


`x(3y - 5) = y + 4`


`3xy - 5x = y + 4`

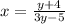
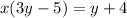
Group like terms to get,


`3xy - y = 5x + 4`

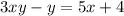
Factor to get,


`y(3x - 1) = 5x + 4`
Solve for y,


`y = (5x + 4)/(3x - 1)`

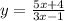
Hence


`{f}^( - 1)(x) = (5x + 4)/(3x - 1)`

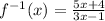
where


`x \\e (1)/(3)`