Question

I need help anyone can anyone help

Answer 1

14

Explanation:

The perimeter is the sum of the sides, so we have

2x+x+15+4x-7=57

= 7x+8

Subtracting 8 from both sides, we get

7x= 49

Dividing 7 from both sides, we get

x=7

Our sides are then 2x=14, x+15=22, and 4x-7=21. 14 is our answer

Answer 2

The shortest length of the triangle is: 14

Hence, option B is correct.

Explanation:

Given the triangle with the lengths

• 
  `x+15`

• 
  `4x-7`

• 
  `2x`

Given that the perimeter of triangle = P = 57

We know that the perimeter of a triangle is the sum of the lengths of the sides of a triangle.

so

`P = (x+15)+(4x-7)+(2x)`

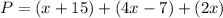
substitute P = 57

`57 = (x+15)+(4x-7)+(2x)`

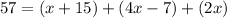
switch sides

`\left(x+15\right)+\left(4x-7\right)+\left(2x\right)=57`

`x+15+4x-7+2x=57`

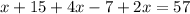
Group like terms

`x+4x+2x+15-7=57`

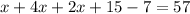
Add similar elements

`7x+15-7=57`

`7x=49`

divide both sides by 7

`(7x)/(7)=(49)/(7)`

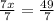
simplify

`x=7`

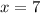
Now, measuring the lengths by substituting x = 7

• 
  `x+15 = 7+15 = 22`

• 
  `4x-7 = 4(7)-7 = 28 - 7 = 21`

• 
  `2x = 2(7) = 14`

Therefore, the shortest length of the triangle is: 14

Hence, option B is correct.