Question

A line of regression y=-1,240 + 7.07x is the best fit line for a set of data comparing airfare with 30 days notice and one-day notice. Find the best predicted cost of a ticket purchased one day in advance given that the cost of the ticket is $300 if purchased 30 day in advance of the flight.

Answer 1

505.03 dollars

Explanation:

Given that
`y=-1,240 + 7.07x`

is the best fit line for y the cost of ticket and x the no of days of notice.

x is independent and y the dependent variable.

0<x<30

Given that cost of ticket is 300 if x =30

y(30) = 300

i.e.

y(1)=?

Since slope of the line is 7.07 for every day increase we get cost increases by 7.07

Hence for 1 day notice we get 29 days difference from 30 days so cost would be

`300+29(7.07)\\=505.03`

Hence predicted value from the regression line is 505.03

Answer 2

$881

Explanation:

Given : A line of regression y=-1,240 + 7.07 x is the best fit line for a set of data comparing airfare with 30 days notice and one-day notice.

To Find: Find the best predicted cost of a ticket purchased one day in advance given that the cost of the ticket is $300 if purchased 30 day in advance of the flight.

Solution:

Line pf Regression :
`y=-1240 + 7.07 x`

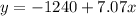
Where x is the cost of a ticket purchased on 30 days notice

y represents the cost of ticket on 1 day notice .

We are given that the cost of ticket was $300 when purchased 30 day in advance of the flight.

So, substitute x = 300

`y=-1240 + 7.07(300)`

`y=881`

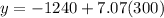
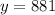
Hence the best predicted cost of a ticket purchased one day in advance given that the cost of the ticket is $300 if purchased 30 day in advance of the flight is $881.