Answer:
In 4.81 minutes the concentration of reactant will drop to 6.25% of the original concentration.
Step-by-step explanation:
Integrated rate law of first order kinetic is given as:
![\log [A]=\log [A_o]-(kt)/(2.303)](https://img.qammunity.org/2020/formulas/chemistry/high-school/tt0g9duna27yvxa9n2x5k6bo3w5r30moc2.png)
Where:
![[A_o]](https://img.qammunity.org/2020/formulas/chemistry/high-school/38eb24kf04xqy5t88y9g0vzh3m04r4nqgg.png) = Initial concentration of reactant
= Initial concentration of reactant
[A] =concentration left after time t .
k = Rate constant
We are given :
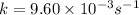
![[A_o]=x](https://img.qammunity.org/2020/formulas/chemistry/high-school/z92ubomolei37qskr9zjxs6hd1wq51ow94.png)
![[A]=6.25% of x =0.0625x](https://img.qammunity.org/2020/formulas/chemistry/high-school/qemos88xipalykxa6353mr6tb3961tcxvm.png)
Time taken during the reaction = t=?
![\log [0.0625 x]=\log[x]-(9.60* 10^(-3) s^(-1)\tmes t)/(2.303)](https://img.qammunity.org/2020/formulas/chemistry/high-school/165fdyqp9fp79th6br0nokewkia68t9ipp.png)
t = 288.86 seconds = 4.81 minutes
1 min = 60 seconds
In 4.81 minutes the concentration of reactant will drop to 6.25% of the original concentration.