Question

Write the Recursive Rule for the sequence:

2, 9, 16, 23, 30,…

Question 1 options:

an=an−1+7, a1=2

an=an−1−7, a1=2

an=an−1+2, a1=7

an=an−1+2, a1=−7

Answer 1

A formula is recursive if it expresses the term
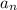`a_n` in terms of the previous one(s)
`a_(n-1),\ a_(n-2),\ \ldots,\ a_1`

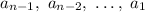
In this case, every term is 7 more than the previous one, so the formula for
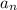`a_n` will only involve
`a_(n-1)`:

`a_n = a_(n-1) + 7`

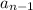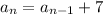
In fact, this formula is simply saying: for every index
`n`, the term with that index is 7 more than the term before.

Also, we have to specify the starting point (otherwise we would go backwards indefinitely), so the complete recursive formula is

`a_n = a_(n-1) + 7,\quad a_1 = 2`

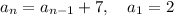
which means: start with 2 and generate every other term by adding 7 to the previous one.