Question

Bob has two weekend jobs last weekend he made a total of $77 after working as a cashier for 5 hours and delivering newspapers for 4 hours this weekend he made $78 working at his cashier job for 6 hours and delivering newspapers for 3 hours how much does he get paid per hour at each job

Answer 1

Answer: $9 per hour at his job as a cashier and $8 per hour at his job delivering newspapers.

Explanation:

1. Let's call the amount he got paid per hour at his job as a cashier:
`x`.

Let's call the amount he got paid per hour at his job delivering newspapers:
`y`.

2. Keeping on mind the information given in the problem above, you can make the following system of equations:

`\left \{ {{5x+4y=77 \atop {6x+3y=78}} \right.`

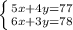
3. You can solve it by applying the Substitution method, as following:

- Solve for one of the variables from one of the equations and substitute it into the other equation to solve for the other variable and calculate its value.

- Substitute the value obtained into one of the original equations to solve for the other variable and calculate its value.

4. Therefore, you have:

`5x+4y=77\\5x=77-4y\\x=(77-4y)/(5)=15.4-0.8y`

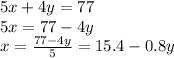
Then:

`6(15.4-0.8y)+3y=78\\92.4-4.8y+3=78\\-1.8y=-14.4\\y=8`

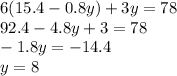
Finally:

`5x+4(8)=77\\5x+32=77\\5x=45\\x=9`

Therefore he got paid $9 per hour at his job as a cashier and $8 per hour at his job delivering newspapers.