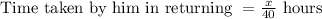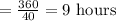Answer: Time taken by him in going = 8 hours
Time taken by him in returning = 9 hours
Explanation:
Let the total distance from home to New York is x miles,
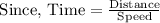
Also, he drove his car from his home to New York at the rate of 45 mph,
⇒
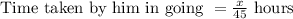
And, returned over the same road at the rate of 40 mph.
⇒
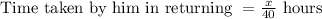
According to the question,
Time taken by him in returning - Time taken by him in going = 30 minutes = 1/2 hours, ( 1 hours = 60 minutes )
⇒
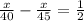
⇒
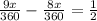
⇒
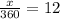
⇒
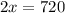
⇒
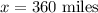
Hence, the total distance from home to New York = x miles = 360 miles
⇒
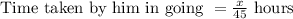
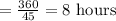
⇒