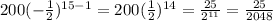Answer:
15th term will be
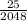
Explanation:
In a geometric progression we know any term of the series is represented as
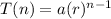
where a = first term, r = common ratio, and n = number of term
Now as per question 4th term is -25 then as pr formula
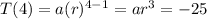 ------(1)
------(1)
Now the ninth term is 25/32
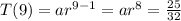 -----(2)
-----(2)
Now we put the value of a from equation 1 to equation 2
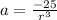
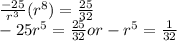
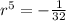
![r = -\frac{1}{\sqrt[5]{32}} = -(1)/(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/dyzo5n70lj8a4y5r23c5uav742qjj5dzd5.png)
therefore a =
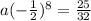
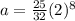
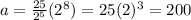
Therefore 15th term will be