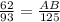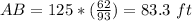Answer:
Part A) The triangles ABC and EDC are similar by AAA, because the three internal angles are equal in both triangles
Part B) The width of the river is about
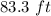
Explanation:
we know that
If two triangles are similar, then the ratio of its corresponding sides is equal and its corresponding angles are congruent
Part A) we know that
In this problem , triangles ABC and CDE are similar by AAA, because its corresponding angles are congruent
so
m<DCE=m<ACB -----> by vertical angles
m<EDC=m<ABC -----> is a right angle
m<DEC=m<CAB -----> the sum of the internal angles must be equal to 180 degrees
Part B) we know that
The triangles ABC and EDC are similar -------> see Part A
therefore
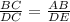
substitute the values and solve for AB