Answer
magnitude of second vector is 871 and it makes angle of 36.019 degrees to the positive x-axis
Solution
In this question we have given
vector 1=

and resultant =

let second vector be V=
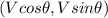
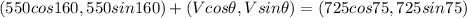
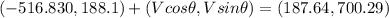
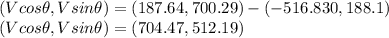 ............(1)
............(1)
on comparing x and y component of both sides of equation 1
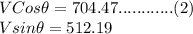 ............(3)
............(3)
Therefore,
divide equation 3 by equation (2)
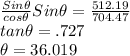
put value of
 in equation (2)
in equation (2)
