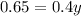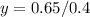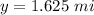Answer:
The other dimension of the pasture (width) is
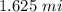
Explanation:
In this problem I assume that the pasture has the shape of a rectangle.
Let
x -----> the length of the pasture
y -----> the width of the pasture
we know that
The area of the pasture (rectangle) is equal to
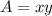
we have
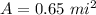
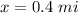
substitute and solve for y