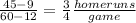Question

The n number of homeruns hit during the regular season by a certain baseball player can be modeled by the function n(x) =3/4x, where x is the number of games that have been played. Find the average rate of change from game 12 to game 60.

Answer 1

The average rate of change is equal to
`(3)/(4)(homeruns)/(game)`

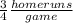
Explanation:

we have

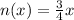`n(x)=(3)/(4)x` -----> this is a linear direct variation

we know that

The rate of change of a linear variation is a constant

The rate of change of a linear variation is equal to the slope of the line

In this problem the slope of the line is equal to
`m=(3)/(4)(homeruns)/(game)`

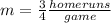
therefore

The average rate of change is equal to
`(3)/(4)(homeruns)/(game)`

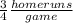
Verify

the average rate of change is equal to

`(n(b)-n(a))/(b-a)`

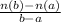
In this problem we have

`n(a)=n(12)=(3)/(4)(12)=9\ homeruns`

`n(b)=n(60)=(3)/(4)(60)=45\ homeruns`

`a=12\ games`

`b=60\ games`

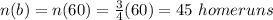
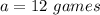
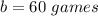
Substitute

`(45-9)/(60-12)=(3)/(4)(homeruns)/(game)`