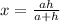Question

I need help asap pls and thank you ;)

Given: △KMN, ABCD is a square
KN=a,
MP
⊥
KN
, MP=h
Find: AB

Answer 1

`\text{Length of AB is }(ah)/(a+h)`

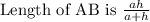
Explanation:

Given △KMN, ABCD is a square where KN=a, MP⊥KN, MP=h.

we have to find the length of AB.

Let the side of square i.e AB is x units.

As ADCB is a square ⇒ ∠CDN=90°⇒∠CDP=90°

⇒ CP||MP||AB

In ΔMNP and ΔCND

∠NCD=∠NMP (∵ corresponding angles)

∠NDC=∠NPM (∵ corresponding angles)

By AA similarity rule, ΔMNP~ΔCND

Also, ΔKAP~ΔKPM by similarity rule as above.

Hence, corresponding sides are in proportion

`(ND)/(NP)=(CD)/(MP) \thinspace\thinspace and\thinspace\thinspace (KA)/(KP)=(AB)/(PM) \\\\(ND)/(NP)=(x)/(h) \thinspace\thinspace and\thinspace\thinspace (KA)/(KP)=(x)/(h)\\\\(NP)/(ND)=(h)/(x) \thinspace\thinspace and\thinspace\thinspace (KP)/(KA)=(h)/(x)\\\\(PD)/(ND)=(h)/(x)-1 \thinspace\thinspace and\thinspace\thinspace (AP)/(KA)=(h)/(x)-1\\`

`KA((h)/(x)-1)=AP`

`ND((h)/(x)-1)=PD`

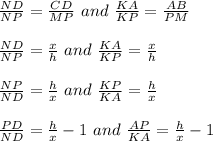
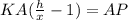
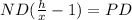
Adding above two, we get

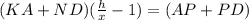
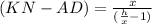
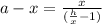
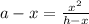
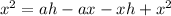
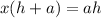
`(KA+ND)((h)/(x)-1)=(AP+PD)`

⇒
`(KN-AD)=(x)/(((h)/(x)-1))`

⇒
`a-x=(x)/(((h)/(x)-1))`

⇒
`a-x=(x^2)/(h-x)`

⇒
`x^2=ah-ax-xh+x^2`

⇒
`x(h+a)=ah`

⇒
`x=(ah)/(a+h)`