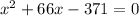Question

Which equation could be used to solve the following system?

Answer 1

`x^2 + 66x -371 = 0`

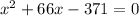
Explanation:

We have two equations:

x + y = 11 (i)

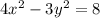`4x^2 - 3y^2 = 8` (ii)

Clear x in equation (i) and substitute it in equation (ii)

`4x^2 -3(11-x)^2 = 8`

`4x^2 -3(121 -22x +x^2) = 8`

`4x^2 -363 + 66x - 3x^2 -8 = 0`

`x^2 + 66x -371 = 0`

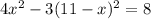
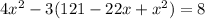
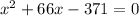
To find the roots of this equation we use the quadratic formula

`(-b +/- √(b^2 - 4ac))/(2a)`

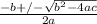
Where:

b = 66

a = 1

c = -371

Then:

`(-66 + √(66^2 - 4(1)(-371)))/(2(1))\\\\and\\\\(-66 - √(66^2 - 4(1)(-371)))/(2(1))`

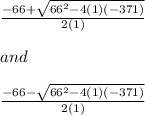
Then the solutions are:

`x = -33 + 2√(365) = 5.21`

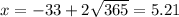
and

`x = -33 - 2√(365) = -71.21`

Finaly, equation could be used to solve the system is
`x^2 + 66x -371 = 0`