Question

A spacecraft on its way to Mars has small rocket engines mounted on its hull; one on its left surface and one on its back surface. At a certain time, both engines turn on. The one on the left gives the spacecraft an acceleration component in the x direction of ax = 5.10 m/s2, while the one on the back gives an acceleration component in the ydirection of ay = 7.30 m/s2. The engines turn off after firing for 675 s, at which point the spacecraft has velocity components of vx = 3630 m/s and vy = 4276 m/s.What was the magnitude and direction of the spacecraft's initial velocity, before the engines were turned on?Express the direction as an angle measured counterclockwise from the x -axis.

Answer 1

v₀ = 677.94 m / s , θ = 286º

Step-by-step explanation:

We can solve this exercise using the kinematic expressions, let's work on each axis separately.

X axis

has a relation of aₓ = 5.10 m / s², the motor is on for a time of t = 675 s, reaching the speed vₓ = 3630 m / s, let's use the relation

vₓ = v₀ₓ + aₓ t

v₀ₓ = vₓ - aₓ t

let's calculate

v₀ₓ = 3630 - 5.10 675

v₀ₓ = 187.5 m / s

Y Axis

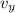`v_(y)` = v_{oy} - a_{y} t

v_{oy} = v_{y} - a_{y} t

let's calculate

v_{oy} = 4276 - 7.30 675

v_{oy} = -651.5 m / s

we can give the speed starts in two ways

a) v₀ = (187.5 i ^ - 651.5 j ^) m / s

b) in the form of module and angle

Let's use the Pythagorean theorem

v₀ =
`\sqrt{v_(ox)^(2) + v_(oy)^(2) }`

v₀ =
`\sqrt{187.5^(2) +651.5^(2) }`

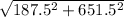
v₀ = 677.94 m / s

we use trigonometry

tan θ =
`(v_(oy) )/(v_(ox) )`

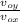
θ = tan⁻¹ \frac{v_{oy} }{v_{ox} }

θ = tan⁻¹ (
`(-651.5)/(187.5)`)

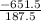θ = -73.94º

This angle measured from the positive side of the x-axis is

θ‘ = 360 - 73.94

θ = 286º