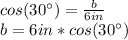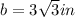Answer: The last option.
Explanation:
The triangle shown in the figure attached is a right triangle.
1. You can calculate the lenght a as following:
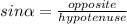
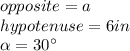
Substitute values and solve for a. Then, you obtain:
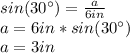
2. You can calculate the lenght b as following:
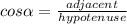
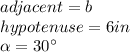
Substitute values and solve for b. Then, you obtain: