Answer:
The statement is false.
Explanation:
The sum of a geometric progression is given by
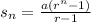
For an infinite GP the sum is given by
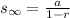
This equation can only be used when the common ratio is less than 1.
Here the statement is in order for an infinite geometric series to have a sum, the common ration has to be greater than one. This statement is wrong because the sum equation can only be used when the common ratio is less than 1.
The statement is false.