Denote the number by
 , where
, where
 are positive integers between 0 and 9
are positive integers between 0 and 9
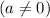 .
.
"the tens digit is two less than the units digit"
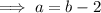
Reversing digits gives a new number
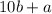 .
.
"sum of the reversed number and the original number is 154"
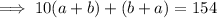
Simplify the second equation:
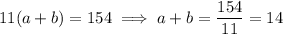
Since
 , by substitution we get
, by substitution we get
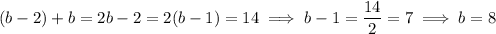
which in turn gives
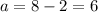
So the original number is
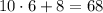 .
.