Answer:
Part A : Total length of Given 3 side =
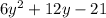
Part B : Length of side 4 =
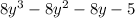
Part C : Yes, Part A & Part B shows that Polynomials are closed under addition and subtraction
Explanation:
Given: Sides of a quadrilateral, Side 1 =
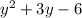 , Side 2 =
, Side 2 =
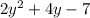 ,
,
Side 3 =
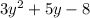 .
.
Perimeter of Quadrilateral =
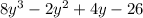
To find: [A] Total length of given 3 sides.
[B] Length of Side 4.
[C] Do part A & B show that the polynomials are closed
under addition and subtraction?
Part A -
Total length of Given 3 side = Side 1 + Side 2 + Side 3
=
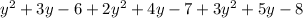
=
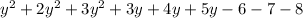
=
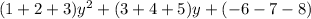
=
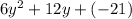
=
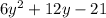
Part B -
Length of side 4 = perimeter - total length of 3 sides
=
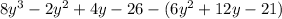
=
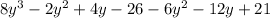
=
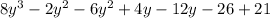
=

=
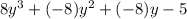
=
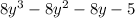
Part C -
Yes, Part A & Part B shows that Polynomials are closed under addition and subtraction because after addition and subtraction result is also a polynomial.