Answer:

Explanation:
We have the equation
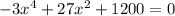
Since it is a polynomial of degree 4, to solve it we must use the ruffini method, as shown below.
We start by testing with x = 5 that it is a multiple of 1200.
-3 0 27 0 1200
5 -15 -75 -240 -1200
--------------------------------------------------
-3 -15 -48 -240 0
x = 5 is a root of the polynomial
Now we try with x = -5
-3 -15 -48 -240
-5 15 0 240
---------------------------------------------
-3 0 -48 0
x = -5 is a root of the polynomial
Then we have the following polynomial
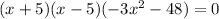
 this polynomial has no real roots
this polynomial has no real roots
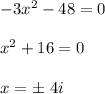
Then we have left:
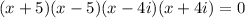
And the zeros of the polynomial are:
