Question

In the following diagram, PQRS is a square of sides 21 cm. PTS and QTR are two semicircles touching each other at T.

Calculate the area, in cm², of the shaded region.
A 94.5 C 141.8 B 113.4 D 189.0 S​

Answer 1

`94.6cm^(2)`

Explanation:

First we will find the area of Square PQRS.

Area of Square PQRS = Length x Width = 21 x 21

=
`441cm^(2)`

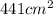
Next we will found the Area of Semicircles PS and QR.

Note: Area of Semicircle PS = Area of Semicircle QR

Area of Semicircle =
`(1)/(2) \pi r^(2)`

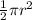
Total Area of Semicircles PS and QR combined =
`2((1)/(2) \pi r^(2) )\\=\pi r^(2)`

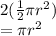
We know that the diameter of PS = QR = 21 cm (due to the length of the square)

Radius = Half of Diameter = 0.5 x 21cm = 10.5cm

Total Area of Semicircles PS and QR =
`\pi (10.5)^(2) \\=110.25\pi cm^(2)`

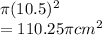
Finally,

Area of Shaded Region = Area of Rectangle PQRS - Total Area of Semicircles PS and QR

=
`441 - 110.25\pi\\= 94.6cm^(2) (1dp)`

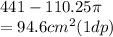
In this case , you can choose the nearest answer as there might be some rounding differences.