For this case, we have to give two points of the form:
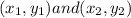
The formula of the midpoint is given by:
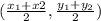
So, be:
(10,3) and (-2, -5)
Substituting in the formula we have:
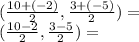
Different signs are subtracted and the greater sign is placed:

(4, -1)
Thus, the midpoint is (4, -1)
Answer:
(4, -1)