Answer:
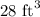
Explanation:
We have been given that a container shaped as a rectangular prism can hold 756 wooden cube blocks with edge lengths of 1/3 ft.
Since the volume is the measure of the amount of space inside of a solid figure. As container holds 756 cubes, so volume of 756 cubes will be equal to the volume of the container.
Since we know that volume of a cube with each side 'a' units is
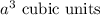 , so the volume of 756 cubes with each edge 1//3 ft will be:
, so the volume of 756 cubes with each edge 1//3 ft will be:
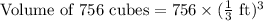
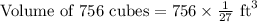
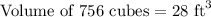
Therefore, the volume of container will be 28 cubic feet.