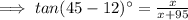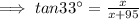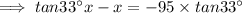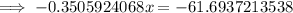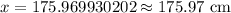Question

At 3pm, the length of the shadow of a thin vertical pole standing on level ground is the same as the height of the pole. A while later, the angle of elevation of the sun has decreased by 12° and the length of the shadow has increased by 95cm. Determine the height of the pole.

Answer 1

Answer: The height of the pole is 175.97 ( approx )

Explanation:

Let the height of the pole is x cm,

Also, let the angle of elevation of the sun to the pole at 3 pm is
`\theta`

Thus, by the question,

`tan\theta = \frac{\text{ The height of the pole}}{\text{ The height of the shadow}}`

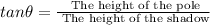
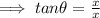`\implies tan\theta = (x)/(x)` ( at 3pm the height of shadow = height of the pole)

`\implies tan\theta = 1`

`\implies \theta = 45^(\circ)`

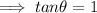
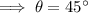
Again, according to the question,

When the angle of elevation is
`(\theta - 12^(\circ))`,

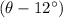The height of shadow = x + 95,

`\implies tan(45-12)^(\circ)=(x)/(x+95)`

`\implies tan 33^(\circ)=(x)/(x+95)`

`\implies tan 33^(\circ)x + 95* tan33^(\circ)=x`

`\implies tan 33^(\circ)x - x = - 95* tan33^(\circ)`

`\implies -0.3505924068 x = - 61.6937213538`

`x=175.969930202\approx 175.97\text{ cm}`