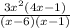Question

[Delete Question]Find the quotient with the necessary restrictions.

16x^2 - 8x + 1. 20x^2 - 5x
--------------------÷ --------------
x^2 - 7x + 12. 15x^3

Answer 1

`(3x^(2)(4x-1))/((x-6)(x-1))`

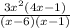
Explanation:

By first factoring the polynomials, we can simplify the expression before completing the operation:

`(16x^(2)-8x +1)/(x^(2)-7x+12)/(20x^(2)-5x)/(15x^(3))`

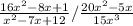
16x² - 8x + 1 = (4x -1)(4x - 1)

x² - 7x + 12 = (x-6)(x-1)

20x² - 5x = 5x(4x -1)

15x³ = 15x³

Since the operation involves dividing two fractions, we can use the rule of keep, change, flip to keep the first fraction, change the sign to multiplication and flip the second fraction:

`((4x-1)(4x-1))/((x-6)(x-1))*(15x^(3))/(5x(4x-1))=(15x^(3)(4x-1)(4x-1))/(5x(4x-1)(x-6)(x-1))`

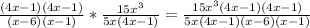
Cancel out the like terms and simplify:

`(3x^(2)(4x-1))/((x-6)(x-1))`