Question

A line contains the points (–2, –6) and (4, 1). Using point-slope form, write the equation of the line that is perpendicular to the given line and that passes through the point (4, 1).

Answer 1

`y-1=-(6)/(7)(x-4)`

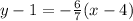
Explanation:

Using the slope formula, substitute the points (-2,-6) and (4,1).

`m=(y_2-y_1)/(x_2-x_1)  = (1--6)/(4--2) =(7)/(6)`

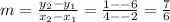
This is the slope of the two points. The slope perpendicular to it will be the negative reciprocal -6/7. Substitute m = -6/7 and the point (4,1) into the point to write the equation of the line.

`y-y_1 = m(x-x_1)\\y-1=-(6)/(7)(x-4)`