Question

The axis of symmetry for a function in the form f(x)= x^2+4x-5 is x=-2 What are the coordinates for the vertex of a graph

Answer 1

(-2-9) is the vertex of the graph.

Explanation:

we have been given a function
`f(x)=x^2+4x-5`

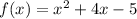
Where, x= -2.

Axis of symmetry is a line on which both sides of the graph is mirror image.

So the graph for the give function is attached in the attachment.

Vertex of symmetry is show with black line and vertex is highlighted which is (-2-9).

Answer 2

`(-2,-9)`

Explanation:

The equation
`f(x)=x^2+4x-5` represents a quadratic function. The graph of a quadratic function is a special type of U-shaped curve called a parabola. By plotting this function, we get the graph of the parabola shown in the figure below.

`The \ vertex \ of \ the \ graph \ of \ f(x)=ax^(2)+bx+c \ is:\\ \\ \left(-(b)/(2a),f\left(-(b)/(2a)\right)\right) \\ \\ \bullet If \ a>0, \ has \ a \ minimum \ at \ x=-(b)/(2a) \\ \\ \bullet If \ a<0, \ has \ a \ maximum \ at \ x=-(b)/(2a)`

So, from the figure you can see that this point is
`(-2,-9)` and since
`a=1>0` this point is a minimum.