Answer:
Plane's speed is 150 miles/hour
Explanation:
Let the plane's airspeed be x
Speed of wind is 30 miles/hour
When a plane flew with the wind , Speed = (x+30)
So, the speed plain with wind on going = (x+30)
Since we are given that on returning plane fly against the wind .
So,When a plane flew against the wind , Speed = (x-30)
So, the speed plain against wind on returning = (x-30)
Distance = 720 miles .
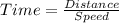
So, time on going
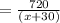
Time on returning
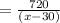
Now we are given that the total time for the whole trip (going + returning) = 10 hours.
So,
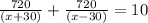
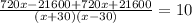
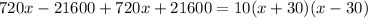
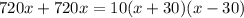
![1440x=10(x^2 -[30]^2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/avmugu1nnk6kjd9fj5cfvqc1g19xze689g.png)
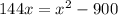
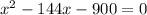
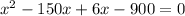
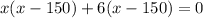
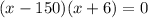
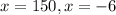
So, the plane's speed is 150 miles/hour