Question

Dave can run the 440 yard dash in 55 seconds, and Jack can run it in 88 seconds. How great a handicap must Dave give Jack for the boys to finish the race at the same time? A. 165 yards B. 242 yards C. 275 yards

Answer 1

For this case we have to, so that both runners finish at the same time, Dave must also reach 88 seconds.

`Dave\ runs\ to\ \frac {440} {55} = 8\ yards\ per\ second\\Jack\ runs\ to\ \frac {440} {88} = 5\ yards\ per\ second`

With respect to the times we have:

`88-55 = 33`

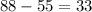
Dave must have a 33-second disadvantage.

This means that in those 33 seconds of difference Jack runs:

`5 * 33 = 165 \ yards`

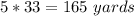
So, Dave must lose 165 yards to get to Jack

Answer:

165