Question

bill traveled to his cabin on the lake and back. It took three hours less time to get there than it did to get back. The average speed on the trip there was 70 mph. The average speed on the way back was 28 mph. How many hours did the trip there

Answer 1

The overall trip takes 30 hours.

Explanation:

Let the time taken on one trip = x ( in hours)

It is given that the time taken on the return trip = (30-x) hours.

As, the average speed for both side of the trips is 70 mph and 28 mph respectively.

Also, as
`Speed=(Distance)/(Time)`

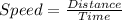
So,
`Distance=Speed* Time`

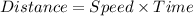
As for both sides of the trip distance will remain same.

We get,

`70x=28(30-x)`

i.e.
`70x=840-28x`

i.e.
`70x+28x=840`

i.e.
`98x=840`

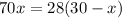
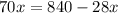
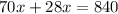
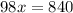
i.e. x= 8.6 hours

So, the time taken for the forward trip is 8.6 hours

Then, the time taken on the return trip is (30-x) = (30-8.6) = 21.4 hours.

Thus, the total number of hours for the round trip = 8.6 + 21.4 = 30 hours.

Hence, the overall trip takes 30 hours.